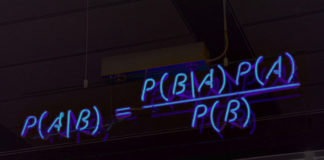A la fin des années 1960, un consensus s’établit dans la communauté scientifique pour minimiser les erreurs d’interprétation dans la présentation de la preuve matérielle. Cela consiste à appliquer un modèle probabiliste, le théorème de Bayes et plus précisément à étudier le rapport de vraisemblance intervenant dans le calcul. Pour évaluer la pertinence d’un résultat analytique dans l’enquête judiciaire, le théorème de Bayes est encore aujourd’hui un modèle acceptable.
A la fin des années 1960, un consensus s’établit dans la communauté scientifique pour minimiser les erreurs d’interprétation dans la présentation de la preuve matérielle. Cela consiste à appliquer un modèle probabiliste, le théorème de Bayes et plus précisément à étudier le rapport de vraisemblance intervenant dans le calcul. Pour évaluer la pertinence d’un résultat analytique dans l’enquête judiciaire, le théorème de Bayes est encore aujourd’hui un modèle acceptable.
Ce modèle utilisé dans d’autres domaines scientifiques, comme la médecine, permet d’évaluer la valeur de l’élément matériel indépendamment de l’élément moral (données d’enquête, témoignages, aveux). Dès 1912, Edmond Locard énonçait le principe selon lequel « L’idéal de l’expertise moderne, telle qu’elle se fait dans les laboratoires, est de réduire l’élément moral de la preuve et d’en augmenter l’élément physique ». Le modèle “Bayesien” permet à la fois au scientifique de rendre compte de la valeur de la preuve matérielle et au juge d’utiliser cette valeur pour favoriser une des deux hypothèses en compétition (Monsieur X est l’auteur du crime, Monsieur X n’est pas l’auteur du crime).
Une critique récurrente de cette approche est la complexité de la méthode et de sa compréhension pour des magistrats ou des jurés. Cependant, les experts sont nommés pour expliquer le plus clairement possible leurs conclusions, et comme le dit Ian Evett en 1991 dans “l’interprétation une odyssée personnelle” :
[pull_quote_center]Les mathématiques sont compliqués car la situation est compliquée, et s’il s’agit de la bonne approche pour interpréter la preuve en criminalistique, alors c’est celle qui doit être utilisée[/pull_quote_center]
L’interprétation de la preuve avec le théorème de Bayes et le modèle “Bayesien”
Comme l’expliquait Poincaré dans son rapport critique à l’égard de Bertillon dans l’affaire Dreyfus, il s’agit de raisonner sur la probabilité des causes et non sur celle des effets. Dans l’investigation, les enquêteurs ou les policiers scientifiques exercent une logique inductive et réalisent des inférences inductives. Ils partent de l’observation des traces et indices et émettent une conclusion sur le déroulement des faits. Cette conclusion n’est pas certaine, elle doit donc être présentée avec des probabilités.
Dans un procès on peut mettre deux hypothèses en compétition :
Hp : Hypothèse du procureur, de l’accusation
Hd : Hypothèse de la défense
L’expert n’a pas connaissance de toutes les circonstances particulières du cas et ne peut pas évaluer correctement les chances en faveur ou en défaveur des hypothèses posées par la cour. L’expert s’exprime donc uniquement sur la valeur de l’indice matériel, à l’aide du “rapport de vraisemblance” ou Likelihood ratio (LR) :
I : Informations générales sur le cas, circonstances de l’affaire
E : Evidence, concordance entre une trace et le matériel de comparaison
P (E/Hp,I) : probabilité d’observer “la trace” sachant l’hypothèse du procureur et les informations du cas
P (E/Hd,I) : probabilité d’observer “la trace” sachant l’hypothèse de la défense et les informations du cas
Le résultat de ce calcul permettra de soutenir une des deux hypothèses mises en opposition :
Si LR = 1 la preuve n’est pas pertinente
Si LR < 1 le résultat soutien l’hypothèse de la défense Hd par rapport à Hp Si LR > 1 le résultat soutien l’hypothèse du procureur Hp par rapport à Hd
Si LR > 1 les hypothèses seront ensuite plus ou moins fortement soutenues en fonction de la valeur du LR.
La probabilité donnée par l’expert est combinée avec la probabilité “a priori” qui est la probabilité d’un évènement avant la phase d’expertise. Cette probabilité est évalué par le juge, les avocats, les jurés à partir des données d’enquête comme des témoignages, aveux…
P (Hp/I) : probabilité de l’hypothèse soutenue par le procureur en fonction des informations générales du cas
P (Hd/I) : probabilité de l’hypothèse soutenue par la défense en fonction des informations générales du cas
En multipliant les deux probabilités précédentes, on obtient la probabilité “à posteriori” qui est la probabilité de la cause après l’avis de l’expert.
P (Hp/E,I) : probabilité de l’hypothèse soutenue par le procureur en fonction des traces retrouvées et des informations générales du cas
P (Hd/E,I) : probabilité de l’hypothèse soutenue par la défense en fonction des traces retrouvées et des informations générales du cas
L’approche Bayesienne permet une évaluation complète en associant l’information analytique de l’expert et l’information, collectée pendant la phase d’enquête, sur les circonstances de l’affaire.
Cette approche clarifie les positions respectives de l’expert et du juge et définit leurs relations : le scientifique se concentrera sur l’évaluation du rapport de vraisemblance et le juge se chargera de l’évaluation des chances a priori et a posteriori.